Programme

Partie structures de données

Contenus

• Arbres : structures hiérarchiques.
• Arbres binaires : nœuds, racines, feuilles, sous-arbres gauches, sous-arbres droits.

Capacités attendues

• Identifier des situations nécessitant une structure de données arborescente.
• Évaluer quelques mesures des arbres binaires (taille, encadrement de la hauteur, etc.).

Commentaires

• On fait le lien avec la rubrique « algorithmique ».

Partie algorithmique

Contenus

• Algorithmes sur les arbres binaires et sur les arbres binaires de recherche.

Capacités attendues

• Calculer la taille et la hauteur d’un arbre.
• Parcourir un arbre de différentes façons (ordres infixe, préfixe ou suffixe; ordre en largeur d’abord).
• Rechercher une clé dans un arbre de recherche, insérer une clé.

Commentaires

• Une structure de données récursive adaptée est utilisée.
• L’exemple des arbres permet d’illustrer la programmation par classe.
• La recherche dans un arbre de recherche équilibré est de coût logarithmique.

Arbres - cas général

Représentation

Pour dessiner des arbres :

• yed-live
• excalidraw

Définition / vocabulaire

Ce vocabulaire est à connaître parfaitement !!

Les arbres permettent de représenter des données avec des notions de parenté ou de hiérarchie.

Un arbre est constitué de noeuds. Chaque noeud peut avoir zéro ou un parent et zéro ou plusieurs enfants.

Si un noeud n’a pas de parent, c’est un noeud racine. Si il n’a pas d’enfants, c’est un noeud terminal.

Un arbre est vide si il ne contient aucun noeud.

Le segment reliant 2 noeuds est une arête.

La profondeur d’un noeud est le nombre de noeuds rencontrés en remontant de ce noeud jusqu’à la racine (en comptant le noeud et la racine) => profondeur de la racine = 1,…

La hauteur d’un arbre est le plus grand nombre de noeuds rencontrés en descendant de la racine jusqu’à une feuille (en comptant la feuille et la racine). On peut aussi dire que c’est la plus grande profondeur de l’arbre.

Autre définition que l’on peut rencontrer : on ne compte pas les noeuds, mais les arêtes pour profondeur et hauteur (=> profondeur de la racine = 0, mais ces définitions posent problème avec les arbres vides)

Arbres binaires

Représentation en diagramme

Définition / vocabulaire

Un arbre binaire est un arbre où chaque noeud a au maximum 2 enfants (gauche et droit). Une définition plus précise sera donnée plus tard dans le cours.

La gauche et la droite sont distinguées, l’ordre des enfants est important.

Structure de données - arbre général

Spécification

Pour représenter un arbre, on a besoin d’une structure de donnée pour chaque noeud, et que chaque noeur puisse contenir l’information :

• soit sur ses enfants (liste d’enfants - c’est le choix qu’on va faire ici, c’est le plus pratique pour manipuler des arbres)
• soit vers son parent (souvent utilisé pour stocker les arbres dans une base de données)
• soit les deux (plus compliqué à gérer car il y a une redondance d’information, et il faut veiller à ce que les deux soient toujours synchronisés)

Pour un noeud Node, on veut avoir la spécification suivante (minimale, mais suffisante pour ce qu’on veut faire) :

• créer un noeud Node (avec valeurs optionnelles pour valeur et enfants)
• ajouter un enfant : Node.add_child(enfant)
• récupérer la liste des enfants : Node.get_children()
• récupérer la valeur du noeud : Noeud.get_value()

Implémentation

from typing import Any, List
class Node:
    def __init__(self, value: Any = None, children: List['Node']| None = None):
        self.__value = value
        if children is None:
            self.__children = []
        else:
            self.__children = children

    def add_child(self, child: 'Node') -> None:
        self.__children.append(child)

    def get_children(self) -> List['Node']:
        return self.__children

    def get_value(self) -> Any:
        return self.__value

Utilisation

Utilisation de la classe Node pour créer un arbre :

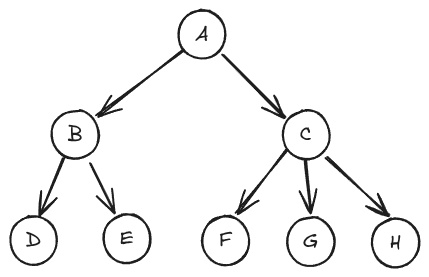
# Création des noeuds (j'utilise des ; pour condenser le code)
na = Node("A")
nb = Node("B"); nc = Node("C")
nd = Node("D"); ne = Node("E")
nf = Node("F"); ng = Node("G"); nh = Node("H")
# Construction de l'arbre (idem)
na.add_child(nb); na.add_child(nc)
nb.add_child(nd); nb.add_child(ne)
nc.add_child(nf); nc.add_child(ng); nc.add_child(nh)
arbre = na # racine de l'arbre

# Création de l'arbre en une seule instruction
arbre = \
  Node("A", [
    Node("B", [
        Node("D"),
        Node("E")
    ]),
    Node("C", [
        Node("F"),
        Node("G"),
        Node("H")
    ])
])

Exercice

Créer les 2 arbres suivants avec la classe Node avec les deux méthodes (création progressive et création en une seule instruction) :

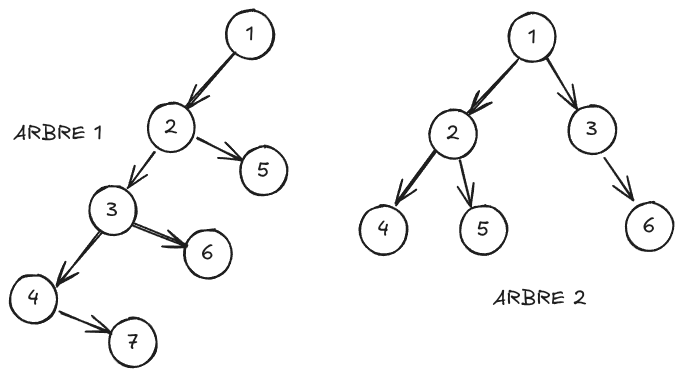
Dessiner les arbres créés par le code suivant :

arbre_1 = \
  Node(1, [
    Node(2, [
        Node(4),
        Node(5, [Node(8),Node(9)])
    ]),
    Node(3, [Node(6),Node(7)])
])

n1 = Node(1); n2 = Node(2); n3 = Node(3)
n4 = Node(4); n5 = Node(5); n6 = Node(6)
n1.add_child(n2)
n1.add_child(n3); n2.add_child(n4)
n2.add_child(n5); n2.add_child(n6)
arbre_2 = n1

Structure de données - arbre binaire

Spécification

Pour un arbre binaire, on peut utiliser une structure de données un peu différente : on ne considère plus une liste d’enfants, mais deux enfants potentiels par noeud : le noeud enfant de gauche et celui de droite.

La gauche et la droite sont distinguées, et l’ordre des enfants est important.

On veut avoir la spécification suivante (minimale, mais suffisante pour ce qu’on veut faire) :

• créer un noeud BinaryNode (avec valeurs optionnelles pour enfant gauche, valeur et enfant droit) : BinaryNode(left=None, value=None, right=None). On peut aussi faire le choix de mettre la valeur en premier, selon la manière dont on veut construire les arbres.
• définir l’enfant gauche : BinaryNode.set_left(child)
• définir l’enfant droit : BinaryNode.set_right(child)
• récupérer l’enfant gauche : BinaryNode.get_left()
• récupérer l’enfant droit : BinaryNode.get_right()
• récupérer la valeur du noeud : BinaryNode.get_value()

Implémentation

from typing import Any, Optional
class BinaryNode:
    def __init__(self, left: Optional['BinaryNode'] = None,
                 value: Any = None,
                 right: Optional['BinaryNode'] = None):
        self.__left = left
        self.__value = value
        self.__right = right
    def set_left(self, child: 'BinaryNode') -> None:
        self.__left = child
    def set_right(self, child: 'BinaryNode') -> None:
        self.__right = child
    def get_left(self) -> Optional['BinaryNode']:
        return self.__left
    def get_right(self) -> Optional['BinaryNode']:
        return self.__right
    def get_value(self) -> Any:
        return self.__value

Utilisation

Utilisation de la classe BinaryNode pour créer un arbre binaire :

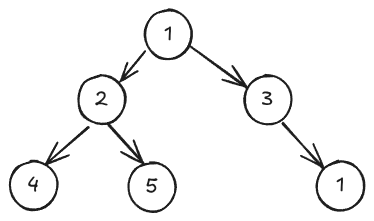
# Création des noeuds (j'utilise des ; pour condenser le code)
n1 = BinaryNode(value=1)
n2 = BinaryNode(value=2); n3 = BinaryNode(value=3)
n4 = BinaryNode(value=4); n5 = BinaryNode(value=5); n6 = BinaryNode(value=6)
# Construction de l'arbre (idem)
n1.set_left(n2); n1.set_right(n3)
n2.set_left(n4); n2.set_right(n5)
n3.set_right(n6)
arbre_binaire = n1 # racine de l'arbre

# Création de l'arbre en une seule instruction
# Si vous inclinez la tête vers la gauche à 90°, vous VERREZ la structure de
# l'arbre !
arbre_binaire = \
  BinaryNode(
    BinaryNode(
        BinaryNode(value=4),
        2,
        BinaryNode(value=5)
    ),
    1,
    BinaryNode(
        None,
        3,
        BinaryNode(value=6)
    )
)

Exercice

Créer les 2 arbres binaires suivants avec la classe BinaryNode avec les deux méthodes (création progressive et création en une seule instruction) :

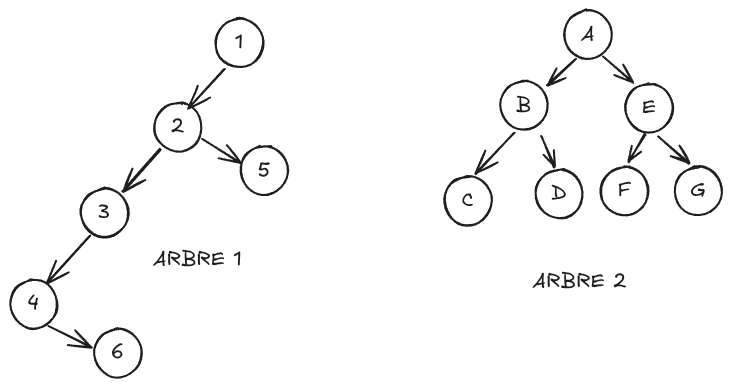
Dessiner les arbres créés par le code suivant :

arbre_binaire_1 = \
  BinaryNode(
    BinaryNode(
        None,
        3,
        BinaryNode(value=4)
    ),
    1,
    BinaryNode(
        BinaryNode(value=6),
        2,
        BinaryNode(value=5)
    )
)

n1 = BinaryNode(1); n2 = BinaryNode(2); n3 = BinaryNode(3)
n4 = BinaryNode(4); n5 = BinaryNode(5); n6 = BinaryNode(6)
n1.set_left(n3)
n1.set_right(n2); n2.set_left(n6)
n2.set_right(n5); n3.set_right(n4)
arbre_binaire_2 = n1

Parcours d’un arbre

Principe

On peut parcourir une structure de données récursive (comme un arbre) en utilisant une fonction récursive : une fonction qui s’appelle elle-même : en effet, pour chaque noeud, les opérations à effectuer sont les mêmes. Donc on peut définir un comportement sur un noeud, puis appliquer ce comportement à chacun de ses enfants en appelant la même fonction.

Un arbre est en effet constitué :

• d’une racine
• et chaque enfant est lui-même un arbre (sous-arbre)

(c’est une définition récursive, on la donnera plus précisement plus tard)

Expérimenter en POV

Se mettre à la place du programme qui fait l’exploration d’un arbre : arbex.educ.space

Vous allez explorer une maison en ouvrant des portes et en entrant dans des pièces. Dans chaque pièce, vous pouvez faire des actions :

• emporter avec vous quelque chose en rentrant dans la pièce
• laisser quelque chose dans la pièce
• emporter quelque chose en sortant de la pièce
• parler à haute voix

Vous savez si vous avez déjà visité une pièce ou pas selon la couleur autour de la porte (verte = déjà visitée), mais à part ça, VOUS N’AVEZ AUCUNE MÉMOIRE NI VUE D’ENSEMBLE DE LA MAISON, vous ne pouvez utiliser que ce que vous voyez (et c’est pour ça que les paroles prononcées sont masquées par défaut, vous ne pouvez pas vous souvenir de ce que vous avez dit avant).

1. Parcourir toute la maison, dès que vous entrez dans une pièce, parlez en annonçant le nom de la pièce (affiché sur le tableau au centre). Puis visitez les portes dans l’ordre où elles apparaissent (de gauche à droite). Vous ne pouvez ressortir de la pièce que lorsque vous avez visité toutes les pièces accessibles depuis cette pièce. Noter à la fin l’ensemble des paroles prononcées.

2. Recommencer, mais cette fois, vous ne parlerez que juste au moment de sortir de la pièce, en annonçant le nom de la pièce. Comparez les paroles prononcées avec celles de l’exercice précédent.

Parcours d’un arbre en python

On peut définir une fonction de parcours récursive qui fait une opération avec le noeud avant de parcourir les enfants (en préfixe) :

def parcours(node: Node) -> None:
    # faire une opération avec le noeud
    print(node.get_value())
    # pour chaque enfant, appeler récursivement la fonction de parcours
    for child in node.get_children():
        parcours(child)

# appel de la fonction de parcours
parcours(arbre)

On peut aussi faire une variante où on fait l’opération après avoir parcouru les enfants (en postfixe) :

def parcours_postfixe(node: Node) -> None:
    # pour chaque enfant, appeler récursivement la fonction de parcours
    for child in node.get_children():
        parcours_postfixe(child)
    # faire une opération avec le noeud
    print(node.get_value())
# appel de la fonction de parcours
parcours_postfixe(arbre)

Comparer les deux parcours.

Algo général récursif

Algorithme récursif global :

• pour un noeud donné (= arbre ou sous-arbre)
• éventuellement effectuer une opération avec le noeud
• pour chaque enfant de ce noeud, appeler récursivement la fonction de parcours pour cet enfant
  • éventuellement en fournissant un ou plusieurs arguments (descente d’information)
  • éventuellement en récupérant des informations de retour de cette fonction (remontée d’information)
• éventuellement effectuer une opération avec le noeud et les éventuels retours de fonction des enfants
• éventuellement retourner une valeur pour la fonction appelante

Descente d’information

• pour un noeud donné (= arbre ou sous-arbre)
• éventuellement effectuer une opération avec le noeud
• pour chaque enfant de ce noeud, appeler récursivement la fonction de parcours pour cet enfant en fournissant un ou plusieurs arguments

Remontée d’information

• pour un noeud donné (= arbre ou sous-arbre)
• pour chaque enfant de ce noeud, appeler récursivement la fonction de parcours pour cet enfant en récupérant des informations de retour de cette fonction
• effectuer une opération avec le noeud et les éventuels retours de fonction des enfants
• retourner une valeur pour la fonction appelante

Parcours d’un arbre binaire

Principe

C’est le même principe que pour un arbre général, mais on a seulement deux enfants à gérer (gauche et droit).

Parcours d’un arbre binaire en python

def parcours_binaire(node: BinaryNode|None) -> None:
    if node is None:
        return
    # faire une opération avec le noeud
    print(node.get_value(), end=' ')
    # appeler récursivement la fonction de parcours avec le noeud gauche
    parcours_binaire(node.get_left())
    # appeler récursivement la fonction de parcours avec le noeud droit
    parcours_binaire(node.get_right())
# appel de la fonction de parcours
parcours_binaire(arbre_binaire)

Autre variante : on vérifie si il y a un enfant avant d’appeler la fonction de parcours :

def parcours_binaire(node: BinaryNode) -> None:
    # faire une opération avec le noeud
    print(node.get_value(), end=' ')
    # appeler récursivement la fonction de parcours avec le noeud gauche
    if node.get_left() is not None:
        parcours_binaire(node.get_left())
    # appeler récursivement la fonction de parcours avec le noeud droit
    if node.get_right() is not None:
        parcours_binaire(node.get_right())
# appel de la fonction de parcours
parcours_binaire(arbre_binaire)

Il existe pour les arbres binaires 3 types de parcours classiques :

• préfixe : on fait l’opération avant d’explorer les enfants
• infixe : on fait l’opération entre l’exploration de l’enfant gauche et droit
• postfixe : on fait l’opération après avoir exploré les enfants

def parcours_prefixe(node: BinaryNode|None) -> None:
    if node is None:
        return
    # faire une opération avec le noeud
    print(node.get_value(), end=' ')
    # appeler récursivement la fonction de parcours avec le noeud gauche
    parcours_prefixe(node.get_left())
    # appeler récursivement la fonction de parcours avec le noeud droit
    parcours_prefixe(node.get_right())

def parcours_infixe(node: BinaryNode|None) -> None:
    if node is None:
        return
    # appeler récursivement la fonction de parcours avec le noeud gauche
    parcours_infixe(node.get_left())
    # faire une opération avec le noeud
    print(node.get_value(), end=' ')
    # appeler récursivement la fonction de parcours avec le noeud droit
    parcours_infixe(node.get_right())

def parcours_postfixe(node: BinaryNode|None) -> None:
    if node is None:
        return
    # appeler récursivement la fonction de parcours avec le noeud gauche
    parcours_postfixe(node.get_left())
    # appeler récursivement la fonction de parcours avec le noeud droit
    parcours_postfixe(node.get_right())
    # faire une opération avec le noeud
    print(node.get_value(), end=' ')

# appel de la fonction de parcours
parcours_prefixe(arbre_binaire)
print()  # pour aller à la ligne
parcours_infixe(arbre_binaire)
print()  # pour aller à la ligne
parcours_postfixe(arbre_binaire)
print()  # pour aller à la ligne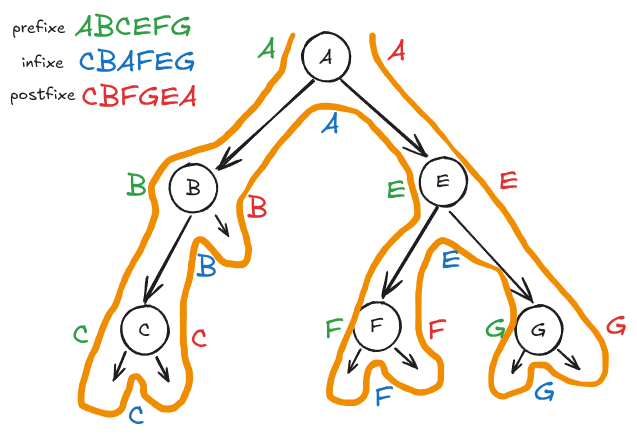

Algo général

Pour un noeud donné

• (éventuellement faire une opération avec le noeud)

• appeler récursivement la fonction de parcours avec le noeud gauche

  • éventuellement en fournissant un ou plusieurs arguments (descente d’information)
  • éventuellement en récupérant des informations de retour de cette fonction (remontée d’information)

• (éventuellement faire une opération avec le noeud ou la valeur retournée)

• appeler récursivement la fonction de parcours avec le noeud droit

  • éventuellement en fournissant un ou plusieurs arguments (descente d’information)
  • éventuellement en récupérant des informations de retour de cette fonction (remontée d’information)

• (éventuellement faire une opération avec le noeud)

• (éventuellement retourner une valeur pour la fonction appelante)

Parcours préfixe

• pour un noeud donné
• faire une opération avec le noeud
• appeler récursivement la fonction de parcours avec le noeud gauche
• appeler récursivement la fonction de parcours avec le noeud droit

Parcours infixe

• pour un noeud donné
• appeler récursivement la fonction de parcours avec le noeud gauche
• faire une opération avec le noeud
• appeler récursivement la fonction de parcours avec le noeud droit

Parcours postfixe

• pour un noeud donné
• appeler récursivement la fonction de parcours avec le noeud gauche
• appeler récursivement la fonction de parcours avec le noeud droit
• faire une opération avec le noeud

Descente d’une information dans l’arbre

• appeler la fonction de parcours avec un argument

Remontée d’une information de l’arbre

• valeur de retour dans la fonction de parcours
• récupération de cette valeur en postfixe et renvoi