Introduction

Exemples

Réseaux sociaux

Réseaux de transport

Internet

Utilisation en informatique

Recherche de chemins

Comment passer d’un état A à un état B

Exploration de graphe

• Recherche d’une meilleure route dans un réseau
• Recherche d’un trajet entre des villes sur une carte

Recherche de cycles

• Recherche de la sortie d’un labyrinthe

Algorithmes

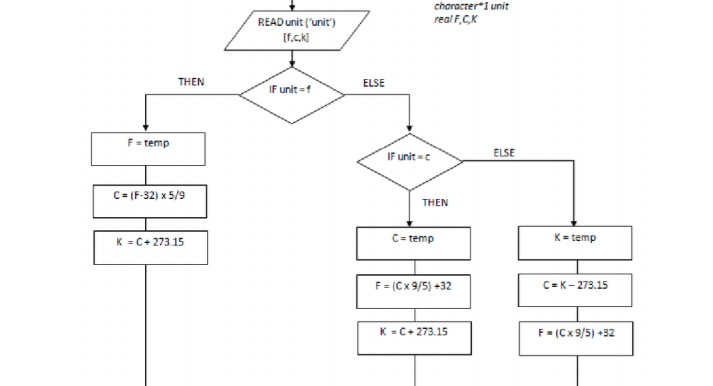
Stockage de données

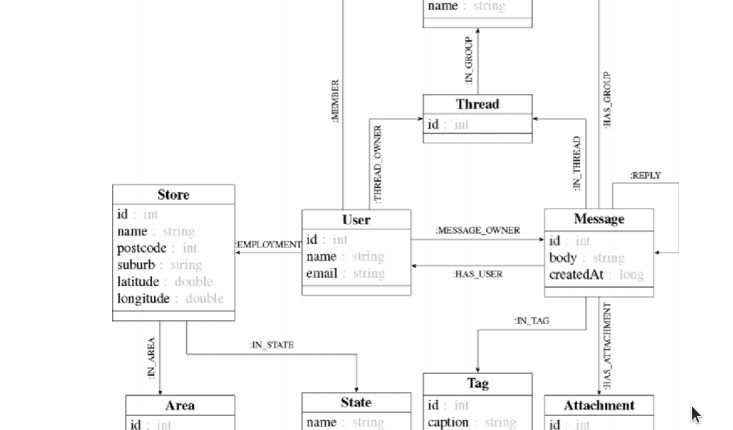
Définitions

Graphe simple

Définition

Un graphe simple est un couple $G=(V,E)$ comprenant

• V un ensemble de sommets (ou noeuds, ou vertice (en))
• E un ensemble d’arêtes reliant ces sommets (ou arcs, ou flèches, ou edge (en))

Une arête est un couple de sommets.

Exemple

Graphe orienté

Définition

Lorsque les arêtes ont une direction (flèche), elles sont orientées

Une arête orientée ne se parcourt que dans le sens de la flèche. Dans ce cas on note généralement les arêtes avec des parenthèses pour désigner des couples.

Si c’est un réseau de transport, on peut se rendre de 1 vers 2, mais pas dans l’autre sens (sens interdit)

Exemple

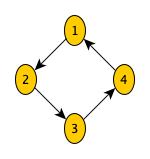
Graphe pondéré

Définition

Toutes les arêtes ne sont pas équivalentes (type de route par exemple)

On attribue un poids (weight) aux arêtes.

Exemple

Voisinage

Définition

Lors qu’il y a un arc d’un sommet s à un sommet t, on dit que t est adjacent à s. Le voisinage d’un sommet est l’ensemble de ses sommets adjacents.

Dans un graphe non orienté, si il y a un chemin de u vers v, il y a aussi un chemin de v vers u, mais ce n’est pas forcément le cas dans un graphe orienté.

Exemple

Donner le voisinage de chacun des sommets du graphe orienté ci-dessous.

Chemin

Définition

Dans un graphe donné, un chemin reliant un sommet u à un sommet v est une séquence finie de sommets reliés deux à deux par des arcs et menant de u à v

Exemple

Donnez 3 chemins reliant 1 à 4 dans le graphe ci-dessous. Y a t’il un chemin entre 5 et 1 ?

Cycle

Définition

Un chemin est dit simple si il n’emprunte pas deux fois le même arc, et élémentaire si il ne passe pas deux fois par le même sommet.

Un chemin simple reliant un sommet à lui-même et contenant au moins un arc est appelé un cycle.

Exemple

Dans le graphe suivant :

• donnez un exemple de chemin non simple
• donnez un exemple de chemin non élémentaire
• donnez un exemple de cycle

Distance

Définition

La longueur d’un chemin est définie comme le nombre d’arcs qui constituent ce chemin. La distance entre deux sommets est la longueur du plus court chemin reliant ces deux sommets. Si aucun chemin n’existe entre deux sommets, la distance n’est pas définie.

La distance d’un sommet à lui-même vaut zéro. Dans un graphe non orienté, la distance d’un sommet u vers un sommet v est la même que la distance entre v et u. Ce n’est pas forcément le cas dans un graphe orienté.

Exemple

Dans le graphe ci-dessous, donnez la distance entre :

• 1 et 4
• 4 et 1
• 5 et 3

Connexité

Définition

On dit qu’un graphe non orienté est connexe si, pour toute paire u,v de sommets, il existe un chemin de u à v.

Pour un graphe orienté, on dit qu’il est connexe si le graphe non orienté obtenu en oubliant le sens des flèches est connexe. On dit qu’il est fortement connexe si il existe un chemin de u vers v sans oublier le sense des flèches.

Exemple

Graphe non orienté non connexe, graphe orienté fortement connexe, graphe orienté connexe.

Implémentations

Introduction

Différence avec arbres

• pas de noeud privilégié
• pas de structure hiérarchique

Il est nécessaire de pouvoir représenter les sommets et les arêtes.

Les sommets peuvent être enregistrés dans n’importe quelle collection (liste, dictionnaire, tuple…)

Pour les arêtes il y a plusieurs possibilités

Ensemble d’arêtes

Collection d’arêtes

On peut donner les arêtes sous la forme d’une collection : [(1,2), (5,8), ...]

• si le graphe est orienté, le sens fait partie de la description des arêtes : (1,2) == de 1 vers 2
• si le graphe est pondéré, on doit stocker le poids dans la liste des arêtes : (1, 2, 12) = de 1 vers 2 avec poids 12

Exemple

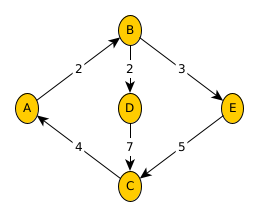
V = ["A", "B", "C", "D", "E"]
E = [("A", "B", 2), ("B", "E", 3),
     ("B", "D", 2), ("D", "C", 7),
     ("E", "C", 5), ("C", "A", 4)]

Arêtes associées aux noeuds

On peut enregistrer dans chaque noeud les arêtes auxquelles il est connecté, éventuellement avec la direction et le poids.

Exemple

E = {
    "A": {"out": [("B", 2)], "in": [("C", 4)]},
    "B": {"out": [("D", 2), ("E", 3)], "in": [("A", 2)]},
    "C": {"out": [("A", 4)], "in": [("D", 7),("E", 5)]},
    "D": {"out": [("C", 7)], "in": [("B", 2)]},
    "E": {"out": [("C", 5)], "in": [("B", 3)]}
}

Matrice d’adjacence

Définition

Une autre représentation des arêtes pour des graphes non pondérés est la matrice d’adjacence

Chaque ligne (horizontal) correspond à un sommet de départ, et chaque colonne (vertical) à un sommet d’arrivée. Si une arête existe entre les deux sommets, on écrit 1, sinon zéro.

Il faut que les sommets soit ordonnés.

Les sommets doivent être ordonnés : A, B, C, D, E

Si le graphe n’est pas orienté, la matrice d’adjacence est symétrique par rapport à sa diagonale.

Exemple

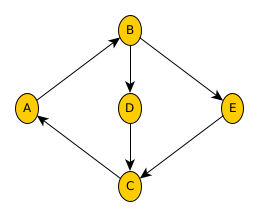
            arrivée
          A B C D E
       A  0 1 0 X 0
       B  0 0 0 1 1
départ C  1 0 0 0 0
       D  0 0 1 0 0
       E  0 0 1 0 0

X = arête partant de A allant vers D ? 0/1

Exercice 1

Ecrire la matrice d’adjacence du graphe suivant

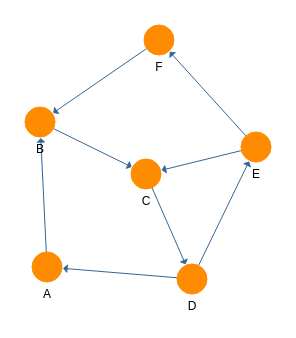
Correction :

0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
1 0 0 0 1 0
0 0 1 0 0 1
0 1 0 0 0 0

Passage d’une forme à l’autre

TP: Ecrire les fonctions python permettant de passer d’une représentation à une autre.