Le programme

Récursivité

Au programme, section [E.2] : Langages et programmation

• Ecrire un programme récursif
• Analyser le fonctionnement d’un programme récursif

Des exemples relevant de domaines variés sont à privilégier. ¹

Exemple : somme des n premiers entiers

Définition classique

On peut écrire la somme des n premiers entiers de la forme :

$$\sum_{i=0}^{i=n}i = 0+1+2+...+n$$

Exemple : pour n=3, on a $0+1+2+3=6$.

Comment créer une fonction somme(n) qui implémente cette formule ? Il faut programmer la répétition (les $+ ... +$)

Boucle for

On peut utiliser une boucle for pour parcourir tous les entiers i entre 0 et n. Il faut donc aussi une variable intermédiaire t pour accumuler la somme des entiers, et retourner la valeur de cette variable à la fin.

def somme(n: int) -> int:
    assert n >= 0, "n doit être positif"
    t = 0
    for i in range(0,n+1):
        t += i
    return t

(le n+1 dans range est nécessaire car la borne supérieure n’est pas incluse)

Difficulté de la définition classique

La formulation mathématique n’indique pas qu’il faut créer une variable t intermédiaire. On peut voir ça de 2 façons :

• c’est la difficulté de la programmation (ou la beauté de l’algorithmique :)
• on peut donner une autre définition mathématique plus “simple”

Formulation récursive

Définition d’une fonction mathématique somme(n) qui, pour tout $n\in\mathds{N}$ renvoie la somme des $n$ premiers entiers :

$$somme(n) = \begin{cases} 0 & \text{si } n=0\\ n+somme(n-1) & \text{si } n > 0\end{cases}$$

Cette définition est récursive : c’est une définition de fonction qui fait appel à elle-même.

Exemple de calculs :

$$\begin{align*} somme(0) & = 0 & & & \\ somme(1) & = 1 + somme(1-1) & = 1 + somme(0) & = 1 + 0 &= 1 \\ somme(2) & = 2 + somme(2-1) & = 1 + somme(1) & = 2 + 1 &= 3 \\ somme(3) & = 3 + somme(3-1) & = 3 + somme(2) & = 3 + 3 &= 6 \end{align*}$$

Avantages de la formulation récursive

Un des avantages est que l’implémentation en python est très proche de la définition de la fonction :

def somme(n: int) -> int:
    assert n >= 0, "n doit être positif"
    if n == 0:
        return 0
    return n + somme(n-1)

Analyse

Exécution du programme pas à pas pour somme(3)

• à la main (déjà fait au dessus, on peut écrire l’arbre d’appel)
• en utilisant pythontutor

À la main : arbre d’appel

Pour calculer somme(3), il faut avoir le résultat de somme(2), qui a besoin du résultat de somme(1), qui a besoin du résultat de somme(0). Le calcul est fait en quelque sorte “à l’envers” : l’arbre d’appel est le suivant :

somme(3) =
    return 3 + somme(2)
                 |
              return 2 + somme(1)
                           |
                        return 1 + somme(0)
                                     |
                                  return 0

Avec pythontutor

Utilisation de https://pythontutor.com/ pour visualiser l’exécution du code, en sélectionnant “show all frames (Python)” dans les options en dessous de “Visualize Execution”

Lien vers pythontutor

Formulations récursives

Définition

Une formulation récursive d’une fonction est toujours constituée de plusieurs cas :

• le ou les cas de base : ils permettent d’obtenir un résultat sans utiliser la fonction en cours de définition (souvent des valeurs particulières pour lesquelles il est facile de déterminer le résultat)
• le ou les cas récursifs : ils font appel à la fonction en cours de définition

Exercice : donner une définition récursive de $x^n$ ($x^n = x\times x\times ... \times x$ $n$ fois, si $n>0$, rappel $x^0=1$), puis écrire son implémentation en python.

Cas de base multiples

Plusieurs cas de base peuvent être donnés :

$$somme(n) = \begin{cases} 0 & \text{si } n=0\\ 1 & \text{si } n=1\\n+somme(n-1) & \text{si } n > 1\end{cases}$$

Cela peut être nécessaire, ou inutile (comme pour l’exemple ci-dessus)

Cas récursifs multiples

Plusieurs cas récursifs peuvent être donnés. Exemple, pour la suite appelée suite de Syracuse : voir wikipedia fr.wikipedia.org/wiki/Conjecture_de_Syracuse et/ou cette vidéo de Veritasium.

On considère la suite définie par un entier $k>0$ (le point de départ) et $n\in\mathds{N}$ (le nombre d’itérations) :

$$sy(n, k) = \begin{cases} k & \text{si } n=0\\ sy(n-1, k)/2 & \text{si } n>=1 \text{ et } sy(n-1, k) \text{ pair}\\ 3\times sy(n-1, k)+1 & \text{si } n>=1 \text{ et } sy(n-1, k) \text{ impair} \end{cases}$$

En mode TLDR pour la conjecture de Syracuse: on suppose qu’on part d’un entier $k>0$; on calcule les termes successifs ($n$) de la suite de Syracuse définie ci-dessous, et on observe que, quelle que soit la valeur de $k$, on finit toujours par atteindre le nombre un $n$ pour lequel la suite atteint 1. Ce nombre $n$ est appelé le temps de vol de $k$. %

Exercice : implémenter def sy(n,k), vérifier son fonctionnement sur quelques valeurs. Puis écrire un programme (non récursif) temps_de_vol(k) appelant sy(n,k) qui détermine le temps de vol pour le nombre k. Enfin, utilisez temps_de_vol sur les 100 premiers entiers pour vérifier la conjecture de Syracuse pour tous les $k<100$.

Double (ou plus) récursion

Les expressions peuvent dépendre de plusieurs appels à la fonction en cours de définition. Exemple, la suite de Fibonnacci : https://fr.wikipedia.org/wiki/Suite_de_Fibonacci

$$fib(n) = \begin{cases} 0 & \text{si } n=0 \\ 1 & \text{si } n=1 \\ fib(n-2) + fib(n-1) & \ \text{ si} n > 1 \end{cases}$$

Exercice : écrire l’arbre d’appel de $fib(5)$; que peut-on dire du nombre d’opérations nécessaires pour calculer fib(n) ? Implémenter fib(n) en python et chronométrer son exécution pour différentes valeurs de n.

Cet exemple “explosif” montre qu’on peut rapidement se retrouver avec des temps de calcul monstrueux avec des implémentations récursives naïves.

Une optimisation possible est de mémoriser les résultats déjà calculés (la technique de la mémoïsation - ce n’est pas une erreur de frappe, c’est bien memoïsation, pas mémorisation). On verra ça plus tard.

Récursion imbriquée

Les appels à la fonction en cours de définition peuvent parfois être imbriqués. Exemple : une fonction complètement tordue : la fonction $f_{91}$ (article wikipedia si vous voulez en savoir plus).

$$f91(n) =\begin{cases} n-10 & \text{si } n > 100,\\ f91(f91(n+11)) & \text{si }n \leq 100. \end{cases}$$

Exercice : évaluer $f_{91}(99)$

Récursion mutuelle

Définition en même temps de deux fonctions récursives s’appelant l’une l’autre.

Exemple : les fonctions est_pair(n) et est_impair(n) qui déterminent si un entier $n$ est pair ou impair.

$$est\_pair(n) = \begin{cases} \text{Vrai} & \text{si } n=0,\\ est\_impair(n-1) & \text{si } n>0. \end{cases}$$

$$est\_impair(n) = \begin{cases} \text{Faux} & \text{si } n=0,\\ est\_pair(n-1) & \text{si } n>0. \end{cases}$$

Définitions récursives bien formées

Règles à respecter

Les règles suivantes doivent être respectées pour qu’une fonction récursive (= avec au moins un cas de base et un cas récursif) soit bien écrite :

• s’assurer que la récursion va bien se terminer (qu’on retombe sur un des case de base)
• s’assurer que les arguments de la fonction sont toujours dans le domaine de la fonction
• s’assurer qu’il y a bien une définition pour toutes les valeurs du domaine.

La vérification de ces règles permet de détecter des erreurs dans les définitions récursives.

Exemples - cas de base non atteint

$$f(n) =\begin{cases} 1 & \text{si } n = 0,\\ n+f(n+1) & \text{si }n \geq 0. \end{cases}$$

Le cas de base n’est jamais atteint.

Exercice: expliquer pourquoi le cas de base n’est jamais atteint.

Exemples - domaine non respecté

$$g(n) = \begin{cases} 1 & \text{si } n=0, \\ n+g(n-2) & \text{si } n> 0. \end{cases}$$

$g(1)$ pose un petit problème…

Exercice : expliquer pourquoi le domaine n’est pas respecté.

Exemple - définitions manquantes

$$h(n) = \begin{cases} 1 & \text{si } n=0,\\ n+h(n-1) & \text{si } n>1. \end{cases}$$

Il manque un truc…

Exercice : expliquer pourquoi la définition est incomplète.

Exercices

Exo 1

La fonction factorielle $n!$ est définie par $n! = 1\times 2\times ···\times n$ si $n > 0$ et $0! = 1$.

1. Donner une définition récursive qui correspond au calcul de la fonction factorielle.
2. Vérifier que votre définition est bien formée (respecte les règles vues précédemment).
3. Écrire en Python le code d’une fonction fact(n) qui implémente cette définition.

Exo 2

1. Écrire une définition récursive d’une fonction nbc(n) qui prend un entier positif ou nul $n$ en argument et renvoie son nombre de chiffres. Par exemple, $nbc(43321)$ doit renvoyer 5. Indice : penser à ce que fait la division entière par 10, et au fait que tous les entiers entre 0 et 9 ont un seul chiffre.
2. Vérifier que votre définition est bien formée (respecte les règles vues précédemment).
3. Écrire en Python le code d’une fonction nbc(n) qui implémente cette définition.

Exo 3

L’algorithme d’Euclide est un des plus anciens algos connus : https://fr.wikipedia.org/wiki/Algorithme_d%27Euclide

Il permet de calculer le PGCD de deux nombres (plus grand commun diviseur). Rappel : le PGCD de deux entiers $a$ et $b$ est le plus grand entier qui divise à la fois $a$ et $b$.

Exemple : le PGCD de 12 et 15 est 3, car 3 est le plus grand entier qui divise à la fois 12 ($3\times4$) et 15 ($3\times5$).

Représentation visuelle du PGCD :

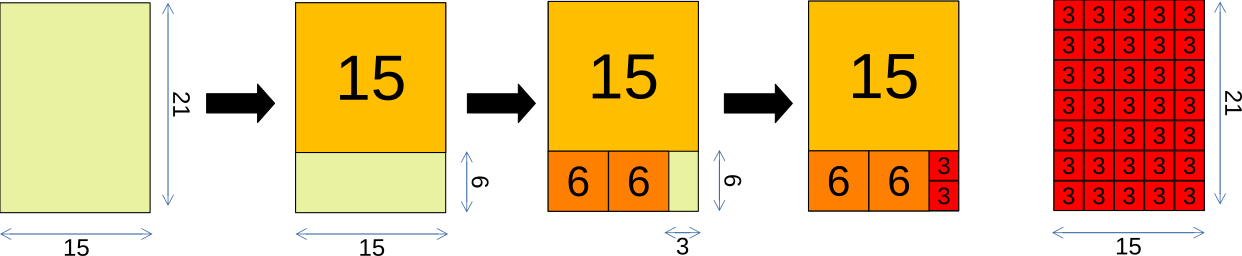
PGCD(a, b) = a si b = 0
           = PGCD(b, a mod b) sinon

1. Identifer le cas de base et le cas récursif
2. Implémenter l’algorithme d’Euclide en python
3. Visualiser sur pythontutor et décrire la pile d’appel pour PGCD(351, 216)