Programme

Partie structures de données

Contenus

Arbres : structures hiérarchiques.
Arbres binaires : nœuds, racines, feuilles, sous-arbres gauches, sous-arbres droits.

Capacités attendues

Identifier des situations nécessitant une structure de données arborescente.
Évaluer quelques mesures des arbres binaires (taille, encadrement de la hauteur, etc.).

Commentaires

On fait le lien avec la rubrique « algorithmique ».

Partie algorithmique

Contenus

Algorithmes sur les arbres binaires et sur les arbres binaires de recherche.

Capacités attendues

Calculer la taille et la hauteur d’un arbre.
Parcourir un arbre de différentes façons (ordres infixe, préfixe ou suffixe; ordre en largeur d’abord).
Rechercher une clé dans un arbre de recherche, insérer une clé.

Commentaires

Une structure de données récursive adaptée est utilisée.
L’exemple des arbres permet d’illustrer la programmation par classe.
La recherche dans un arbre de recherche équilibré est de coût logarithmique.

Arbres binaires

Définition et propriétés

Définitions

Les arbres binaires sont une famille particulière des arbres.

Un arbre binaire non vide est constitué d’un ensemble fini de noeuds correspondant à l’un des deux cas suivants :

Soit l’arbre est vide (il ne contient aucun noeud)
Soit l’arbre n’est pas vide, et ses noeuds sont structurés de la manière suivante :
- un noeud est appelé la racine de l’arbre
- les noeuds restants sont séparés en deux sous-ensembles, qui forment récursivement deux sous-arbres appelés respectivement sous arbre gauche et sous arbre droit
- la racine est reliée à la racine de chacun de ses sous-arbres gauche et droit (lorsqu’ils ne sont pas vides)

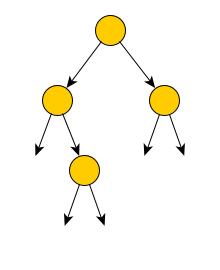
Arbre binaire

Dans un arbre binaire, chaque noeud est donc toujours relié à deux sous-arbres, éventuellement vides.

Lorsqu’un noeud est relié à deux sous-arbres vides, on dit que c’est une feuille, ou un noeud terminal.

La taille d’un arbre (binaire ou non) est son nombre de noeuds.

Exercice :

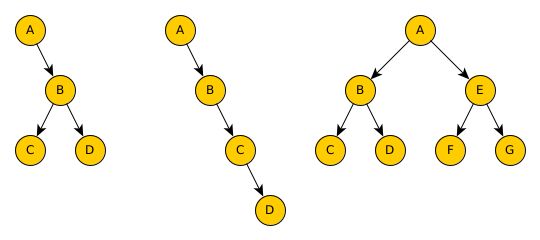
dessiner tous les arbres binaires possédant 4 noeuds.
déterminer la hauteur minimale et maximale des arbres binaires à 4 noeuds

Hauteur d’un arbre

La hauteur d’un arbre (binaire ou non) est le plus grand nombre de noeuds rencontrés en descendant de la racine jusqu’à une feuille (en comptant la feuille et la racine).

La hauteur d’un arbre vide est nulle
La hauteur d’un arbre non vide est la hauteur du maximum des hauteurs de ses deux sous-arbres, plus 1.

Cette définition est plus adaptée que celle comptant le nombre de liens car elle permet de donner une hauteur à un arbre vide.

Si $N$ désigne la taille d’un arbre binaire, et si $h$ désigne sa hauteur, alors :

$h \leq N \leq 2^h-1$

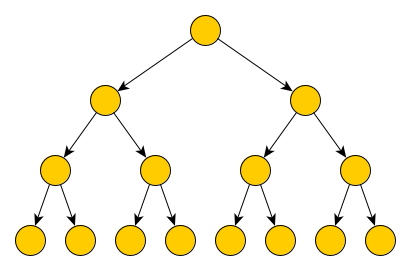
Pour la première partie, on a $h = N$ pour un arbre “linéaire” : cf figure . Les deux extrèmes (que des sous arbres gauches ou droits) sont appelés des peignes.

La deuxième parte, $N=2^h-1$ , est atteinte dans un arbre où toutes feuilles sont exactement à la même hauteur. On appelle ce type d’arbre un arbre parfait (voir figure ).

N=2^h-1 - arbre parfait — $N=2^h-1$ - arbre parfait

Réprésentation en python

Noeud d’un arbre binaire

Un noeud est caractérisé par :

une valeur
sa liaison avec la racine de son sous-arbre droit
sa liaison avec la racine de son sous-arbre gauche

On peut (par exemple) donc le représenter par une classe :

class Node:
    def __init__(self, left, value, right):
        self.value = value
        self.left = left
        self.right = right

Si le sous-arbre droit ou gauche est nul, alors l’attribut left ou right prend la valeur None.

On pourrait aussi rajouter un attribut parent si nécessaire (mais peu utile et compliqué dans les faits).

Exemple :

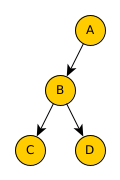
l’arbre de la figure est défini par


a = Node(Node(Node(None,"C",None),
              "B",
              Node(None,"D",None)),
         "A",
         None)

# On peut aussi l'écrire sous une forme plus "arbre"
a = Node(
        Node(
            Node(
                None,
                "C",
                None),
            "B",
            Node(
                None,
                "D",
                None)),
    "A",
    None)

En utilisant pythontutor, on peut visualiser la structure correspondante (figure )

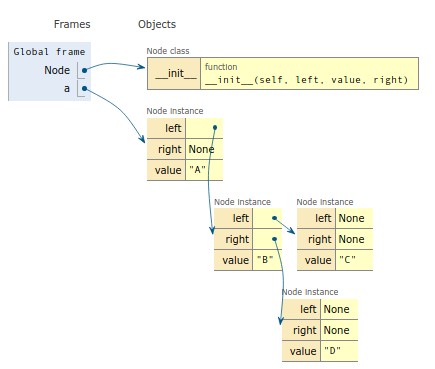
Exercice (python) :

créer en python les 3 arbres de la figure en utilisant la classe Node
vérifier en les visualisant sur pythontutor

Exercice : représenter en python les 3 arbres ci-dessus

Algorithmique des arbres binaires

Opérations récursives

La définition d’un arbre binaire est intrinsèquement récurive (chaque noeud possède deux sous-arbres); la récursivité est donc assez “naturelle” pour effectuer des opérations sur les arbres.

def operation(arbre, paramètres):
    si arbre est vide:
       quitter, éventuellement en renvoyant une valeur
    faire l'opération sur le sous-arbre gauche
        en transmettant éventuellement des paramètres
        en récupérant éventuellement la valeur de retour de l'opération
    faire l'opération sur le sous-arbre droit
        en transmettant éventuellement des paramètres
        en récupérant éventuellement la valeur de retour de l'opération
    quitter, éventuellement en utiliser les résultats
        des sous-arbres et/ou la valeur du noeur pour renvoyer une valeur

Calcul de la taille

def taille(arbre: Node) -> int:
    """Renvoie le nombre de noeuds de l'arbre"""
    if arbre is None:
        return 0
    return 1 + taille(arbre.left) + taille(arbre.right)

Nous avons une fonction doublement récursive. Si la taille de l’arbre est N, alors avec cet algorithme récursif chaque noeud est parcouru une seule fois, et on effectue donc un nombre d’opérations de l’ordre de $2\times N$ , puisque chaque noeud donne lieu à deux additions.

Exercice (python): exécuter cette fonction sur les 3 arbres de la figure en la visualisant sur pythontutor

Calcul de la hauteur

def hauteur(arbre: Node) -> int:
    """Renvoie la hauteur de l'arbre"""
    if arbre is None:
        return 0
    return 1 + max(hauteur(arbre.left), hauteur(arbre.right))

Cet algorithme est très similaire à celui du calcul de la hauteur (de l’ordre de $2N$ opérations)

Exercice (python): comme ci-dessus, exécuter cette fonction sur les 3 arbres de la figure en la visualisant sur pythontutor

Parcours préfixe, infixe, postfixe

Les fonctions taille et hauteur, et de manière générale les fonctions qui vont récursivement parcourir tout l’arbre, peuvent effectuer des opérations avant / après / entre le parcours des sous-arbres gauches et droits. On appelle cela respectivement : parcours prefixe, parcours postfixe, et parcours infixe.


def parcours(arbre: Node):
    if arbre is None:
        return
    # si parcours prefixe :
    # print(a.valeur, end="")
    parcours(arbre.left)
    # si parcours infixe
    # print(a.valeur, end="")
    parcours(arbre.right)
    # si parcours postfixe
    # print(a.valeur, end="")

Le type de parcours dépend du type d’opération que l’on souhaite faire

parcours postfixe si on fait “remonter” une information des feuilles vers la racine
parcours prefixe si on fait “descendre” une information de la racine vers les feuilles

Exercice : effectuer le parcours des 3 arbres de la figure en mode préfixe, infixe et postfixe et constater la différence d’affichage.

Parcours en largeur

Les parcours précédents effectuaient un parcours en profondeur de l’arbre. Si on veut faire un parcours en largeur (visiter tous les noeuds à une hauteur donnée avant de passer à la hauteur suivante), il faut un algorithme différent, utilisant une file (FIFO).

Algorithme de parcours en largeur (non récursif)

mettre le noeud racine dans la file
retirer le noeud du début de la file pour le traiter
mettre tous ses enfants dans la file
si la file n’est pas vide, reprendre à l’étape 2

Implémentation : on va utiliser la classe File basique implémentée dans le chapitre précédent.

class File:
    def __init__(self):
        self.file = list()
    def enfile(self, valeur):
        self.file.append(valeur)
    def defile(self):
        assert len(self.file) > 0, "La file est vide"
        return self.file.pop(0)
    def nbelts(self):
        return len(self.file)

Implémentation en utilisant l’algorithme proposé :

def parcours_largeur(a):
    f = File()
    f.enfile(a)
    while f.nbelts() != 0:
        s = f.defile()
        print(s.value)
        if s.left is not None:
            f.enfile(s.left)
        if s.right is not None:
            f.enfile(s.right)

Exercice : vérifier le fonctionnement de cette fonction parcours_largeur dans pytutor en utilisant les 3 arbres de la figure

Exercices

Exercice 1

Ecrire une fonction affiche(arbre) qui imprime un arbre sous la forme suivante :

si l’arbre est vide, on n’imprime rien
pour un noeud, on imprime successivement
- une parenthèse ouvrante
- son sous-arbre gauche (récursivement)
- sa valeur
- son sous-arbre droit (récursivement)
- une parenthèse fermante

Par exemple, l’arbre de la figure doit afficher (((C)B(D))A)

Exercice 2

Dessiner l’arbre binaire pour lequel le programme précédent produit la sortie (A((B)C)). De manière générale, expliquer comment retrouver la forme de l’arbre dont l’affichage est donné.

Exercice 3

Donner 4 arbres de taille 3, tous différents, pour lesquels le parcours infixe affiche 123.

Exercice 4

Ecrire une fonction indente qui affiche un arbre de manière indentée, en affichant un tiret pour les sous-arbres vides.

Exemple de sortie du programme pour l’arbre de la figure (chaque point · représente un espace)

A
·B
··C
···-
···-
··D
···-
···-
·-

Exercice 5

Ecrire une fonction parfait(h:int) qui prend en argument un nombre entier h supérieur ou égal à zéro et qui renvoie un arbre binaire parfait de hauteur h
Ecrire une fonction peigne_gauche(h:int) qui prend en argument un nombre entier h supérieur ou égal à zéro et qui renvoie un peigne gauche (tous les sous-arbres droits sont vides) de hauteur h
Ecrire une fonction est_peigne_gauche(arbre) qui renvoie True si arbre est un peigne gauche.

Exercice 6

Déterminer quel type de parcours est effecturé si dans la fonction parcours_largeur on remplace la file (FIFO) par une pile (LIFO).

Quel avantage peut-il y avoir par rapport aux méthodes de parcours récursifs ?

Arbres binaires de recherche

Notion d’arbre binaire de recherche

Exemple : organisation d’une bibliothèque

code à 3 lettres : NRS / GHD …
17576 codes, plein de livres avec le même code
1 salle par code, deux sorties par salles

Comment organiser les salles pour trouver rapidement les livres ?

Notion d’arbre binaire de recherche

Un arbre binaire de recherche (ou ABR) est un arbre binaire dont les noeuds contiennent des valeurs qui peuvent être comparées entre elles, et tel que, pour tout noeud de l’arbre :

toutes les valeurs situées dans le sous-arbre gauche sont plus petites que la valeur située dans le noeud.
toutes les valeurs situées dans le sous-arbre droit sont plus grandes que la valeur située dans le noeud.

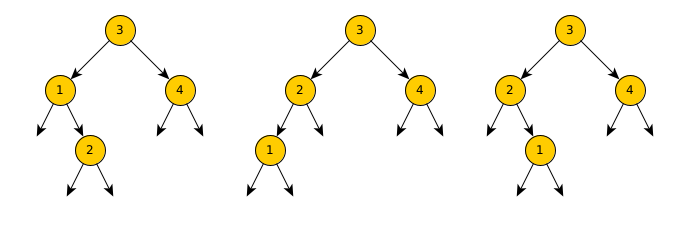
Les deux premiers arbres sont des ABR, celui de droite ne l’est pas. Pourquoi ?

Représentation en python

On utilise juste la représentation Node précédente. Les deux contraintes (valeurs pouvant être compares, et ordre dans l’arbre) sont appliquées dans l’implémentation.

Les fonctions taille, hauteur restent valables pour les ABR.

Le parcours_infixe de l’arbre affiche les éléments dans l’ordre alphabétique.

Exercice 1

Créer 3 arbres binaires de recherche A, B et C contenant les mots :

arbre
pain
zoo
marin
chaleur
souris

Exercice 2

Donner tous les ABR constitués de 3 noeuds et contenant les entiers 1, 2 et 3.

Recherche d’un élément

Principe

On va se diriger dans l’arbre en comparant la valeur à rechercher à la valeur du noeud courant.

si le noeud courant est vide (cas de base), on a rien trouvé => renvoie False
si la valeur à rechercher est strictement plus petite que la valeur du noeud, on va rechercher dans le sous-arbre gauche
si la valeur à rechercher est strictement plus grande que la valeur du noeud, on va rechercher dans le sous-arbre droit
sinon c’est que la valeur à rechercher est égale à la valeur du noeud, on a trouvé et en revoie True.

Programme

def recherche(x, arbre):
    """renvoie True si x est dans l'ABR arbre"""
    if arbre is None:
        return False
    if x < arbre.value:
        return recherche(x, arbre.left)
    if x > arbre.value:
        return recherche(x, arbre.right)
    return True

Exercice 1

Exécuter sous pythontutor la fonction recherche sur les arbres A, B et C de l’exercice précédent, en cherchant soit un mot existant, soit un mot inexistant, et observer le déroulement de la recherche.

Efficacité

On a vu que pour un arbre de taille N, on avant $h \leq N \leq 2^h-1$ avec les deux cas extrèmes des arbres linéaires (dont les peignes) et les arbrs parfaits.

Si l’arbre n’est pas équilibré (au pire, arbre linéaire) on peut avoir une recherche qui parcourt jusqu’à N éléments

Si l’arbre est équilibré (au mieux, arbre parfait), on a une recherche qui parcourra la hauteur de l’arbre équilibré. On a dans ce cas $N=2^h-1$ soit environ $N=2^h$ et donc $h=\log _2(N)=\frac{\ln N}{\ln 2}$

Concrètement, avec une liste de mots de 336000 mots, on aura une recherche en $\log _2(336000)=13$ étapes.

De manière générale, le coût d’une recherche dans un ABR est au pire sa hauteur, et donc dépend grandement de la manière dont il a été construit.

Exercice 2

Dans un ABR, où se trouve le plus petit élémént ? En déduire une fontion minimum(arbre) qui renvoie le plus petit élémént de l’ABR (si l’arbre est vide, cette fonction renvoie None).

Ajout d’un élément

Principe

Dans le principe, ajouter un élément n’est pas plus compliqué que de le rechercher :

si il est plus petit on va à gauche
si il est plus grand, on va à droite
quand on arrive à un arbre vide, on ajoute un noeud

Ajout à un arbre : principe

Solution 1 - modification en place

def ajoute(arbre, elt):
    if elt < arbre.value:
        if arbre.left is None:
            arbre.left = Node(None, elt, None)
            return
        ajoute(arbre.left, elt)
    if elt > arbre.value:
        if arbre.right is None:
            arbre.right = Node(None, elt, None)
            return
        ajoute(arbre.right, elt)

Problème : si l’arbre est vide, notre fonction ajoute ne fonctionne pas.

Exemple avec solution 1

import random

with open("corpus2.txt", "r") as l:
    lines = [m[:-1] for m in l.readlines()]
random.shuffle(lines)

arbre = None
start = time.clock()
for mot in lines:
    if arbre is None:
        arbre = Node(None, mot, None)
    else:
        ajoute(arbre, mot)
print(f"Durée : {time.clock()-start:2.2f}")

Durée : 4.82s

Solution 2 - noeuds immuables

On peut résoudre ce problème en ne modifiant pas l’arbre en place, mais en renvoyant de nouveaux noeuds à chaque fois.

def ajoute(a, elt):
    """ ajoute elt à l'arbre a, renvoie un nouvel arbre """
    if a is None:
        return Node(None, elt, None)
    if elt < a.value:
        return Node(ajoute(a.left, elt), a.value, a.right)
    if elt > a.value:
        return Node(a.left, a.value, ajoute(a.right, elt))
    return Node(a.left, a.value, a.right)

Exemple avec solution 2

import random
import time
with open("corpus2.txt", "r") as l:
    lines = [m[:-1] for m in l.readlines()]
random.shuffle(lines)
arbre = None
start = time.clock()
for mot in lines:
    arbre = ajoute2(arbre, mot)
print(f"Durée : {time.clock()-start:2.2f}")

Durée : 12.51s

Comparaison

La solution 1 est moins élégante, mais plus rapide que la 2 (13 secondes contre 5 secondes environ pour 336000 mots). En effet, il faut rajouter le temps d’allocation en mémoire de la création d’un nouveau noeud.

Solution 1bis

On peut renvoyer à chaque fois l’arbre, de manière “mixer” la création de nouveau noeud pour l’arbre vide et la modification en place pour un arbre existant.

def ajoute(arbre, elt):
    if arbre is None:
        return Node(None, elt, None)
    if elt < arbre.value:
        if arbre.left is None:
            arbre.left = Node(None, elt, None)
        else:
            ajoute(arbre.left, elt)
    if elt > arbre.value:
        if arbre.right is None:
            arbre.right = Node(None, elt, None)
        else:
            ajoute(arbre.right, elt)
    return arbre

Eléments déjà présents

Dans les implémentations précédentes, si un élément est déjà présent, il n’est pas rajouté une deuxième fois à l’ABR. Notre ABR crée donc un ensemble (par définition, un ensemble comporte un exemplaire unique de chaque élément).

On peut avoir besoin d’un multiensemble. Dans ce cas on peut modifier la fonction ajout pour que chaque élément soit systématiquement ajouté.

Efficacité / arbre équilibré

L’ajout tel que nous l’avons implémenté est comparable à la recherche.

Selon la manière dont est construit un ABR, sa hauteur (et donc le nombre d’opérations à faire pour une recherche ou un ajout) peut varier ( $h \leq N \leq 2^h-1$ soit $ln(N) \leq h \leq N$ )

Pour N = 336000, on a donc $13 \leq h \leq 336000$ !

Si la hauteur est trop grande, on ne pourra même pas rechercher, le python déclenchant une exception RecursionError.

L’idéal est de s’approcher au mieux d’un arbre parfait. On dit alors que l’arbre est équilibré.

Construction d’un arbre équilibré

En gros, le principe (pas au programme) est de réorganiser pendant la construction la structure de l’ABR pour éviter que la hauteur ne devienne trop grande.

On peut montrer que si les éléments à ajouter sont “mélangés”, on s’approche pas trop mal d’un arbre équilibré (c’est ce que nous avons fait avec le random.shuffle)

Exercice 1

En vous inspirant des fonctions ajoute précédentes, créer une fonction majoute qui crée un multiensemble si des doublons sont présents.

Exercice 2

Créer une fonction remplir(arbre, liste) qui ajoute tous les éléments de l’arbre arbre dans la liste liste, dans l’ordre infixe.

Utiliser cette fonction pour créer une fonction trier(liste) qui reçoit en argument une liste d’entiers mélangés et renvoie une liste triée contenant les mêmes éléments.

Remarque : selon la fonction d’ajout choisie, la liste renvoyée sera non seulement triée, mais aussi dédupliquée.

Discuter de l’efficacité de cette maniere de trier.