Programme

Partie structures de données

Programme

Contenus

• Graphes : structures relationnelles
• Sommets, arcs, arêtes, graphes orientés ou non orientés

Capacités attendues

• Identifier des situations nécessitant une structure de données arborescente.
• Evauer quelques mesures des arbres binaires (taille, encadrement de la hauteur, etc..)

Commentaires

• On fait le lien avec la rubrique “algorithmique”

Partie algorithmique

Programme

Contenus

• Algorithmes sur les graphes

Capacités attendues

• Parcourir un graphe en profondeur d’abord, en largeur d’abord
• Repérer la présence d’un cycle dans un graphe
• Chercher un chemin dans un graphe

Commentaires

• Le parcours d’un labyrinthe et le routage dans Internet sont des exemples d’algorithmes sur les graphes.
• L’exemple des graphes permet d’illustrer l’utilisation des classes en programmation

Rappel des définitions

Graphe simple

Définition

Un graphe simple est un couple $G=(V,E)$ comprenant

• V un ensemble de sommets (ou noeuds, ou vertice (en))
• E un ensemble d’arêtes reliant ces sommets (ou arcs, ou flèches, ou edge (en))

Une arête est un couple de sommets.

Exemple

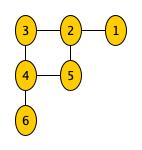
Graphe orienté

Définition

Lorsque les arêtes ont une direction (flèche), elles sont orientées

Une arête orientée ne se parcourt que dans le sens de la flèche. Dans ce cas on note généralement les arêtes avec des parenthèses pour désigner des couples.

Si c’est un réseau de transport, on peut se rendre de 1 vers 2, mais pas dans l’autre sens (sens interdit)

Exemple

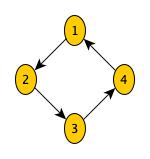
Graphe pondéré

Définition

Toutes les arêtes ne sont pas équivalentes (type de route par exemple)

On attribue un poids (weight) aux arêtes.

Exemple

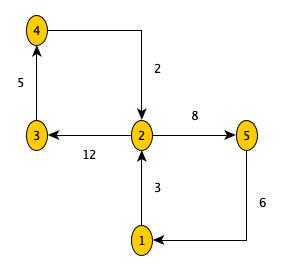
Voisinage

Définition

Lors qu’il y a un arc d’un sommet s à un sommet t, on dit que t est adjacent à s. Le voisinage d’un sommet est l’ensemble de ses sommets adjacents.

Dans un graphe non orienté, si il y a un chemin de u vers v, il y a aussi un chemin de v vers u, mais ce n’est pas forcément le cas dans un graphe orienté.

Exemple

Donner le voisinage de chacun des sommets du graphe orienté ci-dessous.

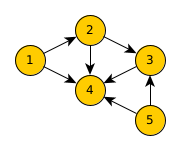
Chemin

Définition

Dans un graphe donné, un chemin reliant un sommet u à un sommet v est une séquence finie de sommets reliés deux à deux par des arcs et menant de u à v

Exemple

Donnez 3 chemins reliant 1 à 4 dans le graphe ci-dessous. Y a t’il un chemin entre 5 et 1 ?

Cycle

Définition

Un chemin est dit simple si il n’emprunte pas deux fois le même arc, et élémentaire si il ne passe pas deux fois par le même sommet.

Un chemin simple reliant un sommet à lui-même et contenant au moins un arc est appelé un cycle.

Exemple

Dans le graphe suivant :

• donnez un exemple de chemin non simple
• donnez un exemple de chemin non élémentaire
• donnez un exemple de cycle

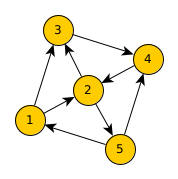
Distance

Définition

La longueur d’un chemin est définie comme le nombre d’arcs qui constituent ce chemin. La distance entre deux sommets est la longueur du plus court chemin reliant ces deux sommets. Si aucun chemin n’existe entre deux sommets, la distance n’est pas définie.

La distance d’un sommet à lui-même vaut zéro. Dans un graphe non orienté, la distance d’un sommet u vers un sommet v est la même que la distance entre v et u. Ce n’est pas forcément le cas dans un graphe orienté.

Exemple

Dans le graphe ci-dessous, donnez la distance entre :

• 1 et 4
• 4 et 1
• 5 et 3

Connexité

Définition

On dit qu’un graphe non orienté est connexe si, pour toute paire u,v de sommets, il existe un chemin de u à v.

Pour un graphe orienté, on dit qu’il est connexe si le graphe non orienté obtenu en oubliant le sens des flèches est connexe. On dit qu’il est fortement connexe si il existe un chemin de u vers v sans oublier le sense des flèches.

Exemple

Graphe non orienté non connexe, graphe orienté fortement connexe, graphe orienté connexe.

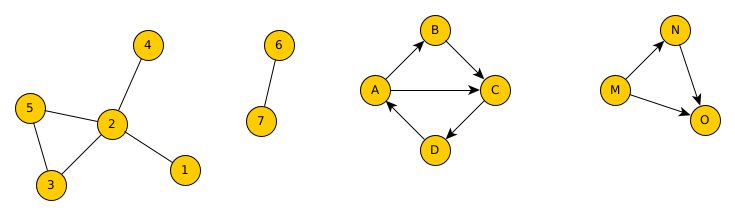
Parcours en profondeur

Principe

Exemple d’un labyrinthe

L’idée du parcours en profondeur est basée sur le principe suivant, appliquable par exemple à la recherche de la sortie dans un labyrinthe :

1. on marque les endroits par lesquels on est déjà passé
2. quand on arrive à un embranchement par lequel on est déjà passé, on fait comme si il s’agissait d’un cul de sac et on revient en arrière jusqu’à la précédente intersection où l’on avait plusieurs choix

Principe général

• on “marque” les sommets par lesquels on est passé
• on parcours chaque direction non déjà explorée

Implémentation récursive

Représentation

Il y a beaucoup de manières de représenter un graphe; la seule chose dont on ait besoin pour le parcours en profondeur, c’est de pouvoir trouver tous les voisins d’un noeud donné (ce qui est indiqué voisins_de_s dans le code ci-après

Implémentation

def parcours(graphe, vus, sommet):
    """ Parcours en profondeur du graphe depuis le sommet s

    :param graphe: graphe
    :param vus: liste des sommets déjà vus
    :param s: sommet de départ
    """

    if s not in vus:
        vus.append(s)
        for v in voisins_de_s:
            parcours(graphe, vus, v)

Terminaison et efficacité

Comment peut-on s’assurer que le parcours s’arrêtera un jour ?

Pour un graphe avec N sommets, quel est le coût du parcours en profondeur ?

Exercice

Effectuer à la main toutes les étapes du parcours en profondeur de l’arbre suivant

Exercice

0,1,0,1,0,0
0,0,0,0,0,1
1,0,0,1,0,1
0,0,1,0,0,0
0,1,0,1,0,1
1,0,1,0,1,0

1. Dessiner le graphe représenté par la matrice d’adjacence ci-dessus
2. Créer une fonction voisin_de(graphe, s) qui utilise la matrice d’adjacence pour renvoyer tous les voisins u somme s
3. Implémenter et effectuer le parcours du graphe

Vous pouvez vérifier vos résultats sur https://graphonline.ru/fr/

Implémentation non récursive

Principe

Si un graphe comporte trop de sommets, on peut dépasser la profondeur de récursion maximale (environ 1000 ou 2000 en python)

Comme pour les arbres, on peut aussi faire un parcours en profondeur en utilisant une pile.

Implémentation

def parcours(graphe, vus, s):
    pile = Pile()
    pile.empile(s)
    while not pile.est_vide():
        s = pile.depile()
        if s in vus:
            continue
        vus.append(s)
        for v in voisins_de_s:
            pile.empile(v)

Exercice

Un utilisant la classe Pile réalisée plus tôt dans l’année, implémentez le parcours de l’arbre de l’exercice précédent.

Détection de cycle

Principe

Parcours en profondeur et cycles

Le parcours en profondeur permet de détecter la présence d’un cycle dans un graphe orienté. En effet, quand on tombe sur un sommet déjà visité, il peut s’agir d’un cycle.

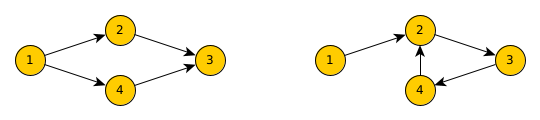
Dans le premier graphe, le parcours fait d’abord 1 2 3 puis 1 4 et détecte qu’il est déjà passé sur 3, mais ce n’est pas un cycle.

Dans le deuxième graphe, le parcours fait 1 2 3 4 puis détecte qu’il est déjà passé par 2; et dans ce cas c’est un cycle

Coloriage des noeuds

Pour savoir si un noeud déjà atteint est marqué à cause d’un parcours multiple ou d’un cycle, on va “colorier” les noeuds avec différentes couleurs :

• blanc si le noeud n’a jamais été visité
• gris si le noeud a été visité, mais pour lequel le parcours en profondeur n’est pas encore terminé
• noir si le noeud a été visité, et si son parcours en profondeur est terminé

Ceci permet de savoir si un noeud déjà rencontré est dû à un cycle ou bien à un chemin multiple :

• si on croise un noeud noir, c’est dû un parcours multiple
• si on croise un noeud gris, c’est dû à un cycle

Exercice

Coloriez et détectez les cycles dans les graphes suivants

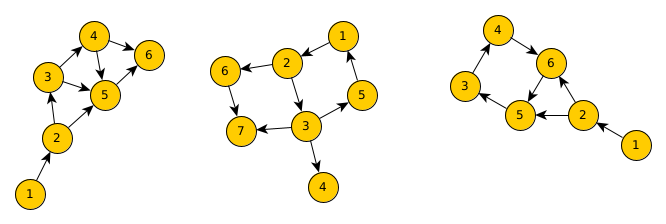
Implémentation

On a besoin de la liste des sommets du graphe sommets_du_graphe et des voisins de chaque sommet (comme précédemment).

On utilise un dictionnaire avec comme clef chaque sommet et comme valeur la couleur de chaque sommet.

BLANC, GRIS, NOIR = 1, 2, 3
def parcours_cycle(graphe, couleurs, s):
    # Détection de cycle ou chemin multiple
    if couleurs[s] == GRIS:
        return True
    if couleurs[s] == NOIR:
        return False

    # Sommet nouveau, on le colorie en gris
    couleur[s] = GRIS
    # On parcourt ses voisins (et on quitte si on a trouvé un cycle)
    for v in voisins_de_s:
        if parcours_cycle(graphe, couleurs, v):
            return True
    # On a fini toute l'exploration de ce sommet => colorié en noir
    couleurs[s] = NOIR
    return False

def cycle(graphe):
    # On prépare la peinture
    couleur = {}
    for s in sommets_du_graphe:
        couleur[s] = BLANC

    # On teste l'existence de cycle pour tous les sommets
    for s in sommets_du_graphe:
        if parcours_cycle(graphe, couleur, s):
            return True
    return False

Terminaison et efficacité

Comment peut-on s’assurer que la recherche de cycle s’arrêtera un jour ?

Pour un graphe avec N sommets, quel est le coût de la recherche de cycle ?

Exercice

Implémenter et lancer la recherche de cycle sur les 3 exemples de graphes de l’exercice précédent.

Recherche du plus court chemin

Algorithme de Dijkstra

Introduction

On a souvent besoin de chercher le chemin le plus “court” entre deux sommets d’un graphe :

• le chemin le plus court (en temps de trajet) entre une ville et une autre
• le chemin le plus court (en distance) entre une ville et une autre
• le chemin le plus court (au sens métrique OSPF) dans un réseau
• le chemin le plus court entre l’entrée et la sortie d’un labyrinthe

Algorithme

Pour des graphes avec des poids positifs, on utilise fréquemment l’algorithme de Dijkstra (parcours en largeur)

https://fr.wikipedia.org/wiki/Algorithme_de_Dijkstra